Introduction
Quick sort or quicksort (sometimes called partition-exchange sort) is an efficient and very fast sorting algorithm for internal sorting, serving as a systematic method for placing the elements of an array in order.
When implemented well, it can be about two or three times faster than its main competitors, merge sort and heapsort.
In efficient implementations it is not a stable sort, meaning that the relative order of equal sort items is not preserved.
Quick sort can operate in-place on an array, requiring small additional amounts of memory to perform the sorting.
Quick sort is a divide and conquer algorithm. Quick sort first divides a large array into two smaller sub-arrays: the low elements and the high elements. Quick sort can then recursively sort the sub-arrays.
The steps for sorting elements using quick sort are as follows:
- Pick an element, called a pivot, from the array.
- Partitioning: reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
- Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.
The base case of the recursion is arrays of size of zero or one, which are in order by definition, so they never need to be sorted.
The pivot selection and partitioning steps can be done in several different ways; the choice of specific implementation schemes greatly affects the algorithm’s performance.
Pictorial Representation
Pictorial representation of quick sort can be given using the following animation (image from Wikipedia):
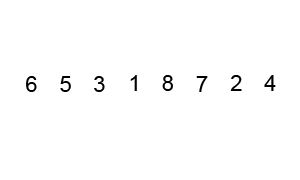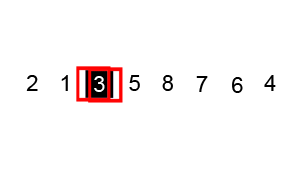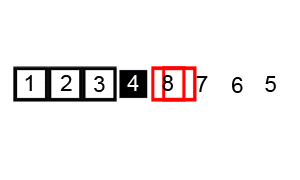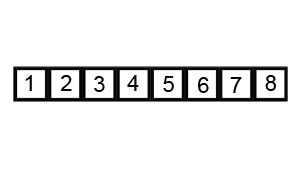
Time Complexity
Worst Case Time Complexity : O(n2)
Best Case Time Complexity : O(n log n)
Average Time Complexity : O(n log n)
Quick Sort Implementation
Here in the below source code we first find the pivot element from an array of elements. We then recursively call the function quickSort () to achieve the final results.
/*
* File: QuickSort.c
* Author: https://roytuts.com
*/
#include <stdio.h>
#include <stdlib.h>
void quickSort(int a[], int low, int high) {
int pi;
if (low < high) {
pi = partition(a, low, high);
quickSort(a, low, pi - 1);
quickSort(a, pi + 1, high);
}
}
int partition(int a[], int low, int high) {
int l, u, pivot, temp;
l = low;
u = high + 1;
pivot = a[l];
while (u >= l) {
while (a[++l] < pivot);
while (a[--u] > pivot);
if (u > l) {
swap(&a[l], &a[u]);
}
}
swap(&a[low], &a[u]);
return u;
}
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}
int main() {
int i;
int a[] = {15, 8, 17, 12, 38, 19};
int n = sizeof (a) / sizeof (a[0]);
printf("\n:: Quick Sort ::\n");
printf("\nInput array elements\n");
for (i = 0; i < n; i++) {
printf("a[%d]=%d ", i, a[i]);
}
quickSort(a, 0, n - 1);
printf("\n");
printf("\nThe sorted array elements are given below\n");
for (i = 0; i < n; i++) {
printf("a[%d]=%d ", i, a[i]);
}
}Testing the Program
By executing the above C program we will get the following output:
:: Quick Sort ::
Input array elements
a[0]=15 a[1]=8 a[2]=17 a[3]=12 a[4]=38 a[5]=19
The sorted array elements are given below
a[0]=8 a[1]=12 a[2]=15 a[3]=17 a[4]=19 a[5]=38