Solving Josephus Problem using Java

Introduction

The Josephus problem (or Josephus permutation) is a theoretical problem related to a certain counting-out game. The problem is described as below.

People are standing in a circle waiting to be executed. Counting begins at a specified point in the circle and proceeds around the circle in a specified direction. After a specified number of people are skipped, the next person is executed.

The procedure is repeated with the remaining people, starting with the next person, going in the same direction and skipping the same number of people, until only one person remains, and is freed.

The pictorial representation of the Josephus problem can be shown in the below image:

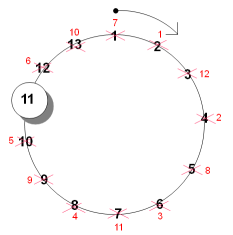
In the above image the execution starts from 2 and finally the free person will be 11.

Related Posts:

Josephus Implementation

The source code using Java programming language is given below:

import java.util.List;
import java.util.stream.Collectors;
import java.util.stream.IntStream;

public class JosephProblem {

	public static void main(String[] args) {
		int winner = joseph(5, 3);
		System.out.println("winner is " + winner);
		winner = joseph(10, 3);
		System.out.println("winner is " + winner);
		winner = joseph(5, 2);
		System.out.println("winner is " + winner);
		winner = joseph(7, 3);
		System.out.println("winner is " + winner);
	}
	
	public static int joseph(int noOfPeople, int remPosition) {
		int tempPos = remPosition - 1;
		int[] people = new int[noOfPeople];
		
		for (int i = 0; i < noOfPeople; i++) {
			people[i] = i + 1;
		}
		
		int iteration = noOfPeople - 1;
		
		List<Integer> list = IntStream.of(people).boxed().collect(Collectors.toList());
		
		while (iteration > 0) {
			list.remove(tempPos);
			tempPos += remPosition - 1;
			if (tempPos > list.size() - 1) {
				tempPos = tempPos % list.size();
			}
			iteration--;
		}
		
		return list.get(0);
	}
	
}

Ananlysis of the Logic

Let’s take an example of there are 5 people in a circle and execution starts clockwise at position 3, so I will find out the winner of the game.

So there are five people – 1 2 3 4 5 and execution starts clockwise at position 3. Therefore if you kill 3 then are left with the list something like – 1 2 4 5.

Now again you have to kill the person at position 3 clockwise counting from the last killed person.

Now you need to execute the person at position 1. So executing the person at 1 you are left with the list 2 4 5. After executing another person you get list 2 4.

Now you are left with 2 persons in the list. So you have to calculate the position wisely to execute the person. Therefore the calculated position would be (starting position of the execution)%(no of people remaining in the list less than starting position) = 3%2 = 1.

So finally the winner is 4.

Recursive Program

The problem can be solved using recursive way as shown below:

public static int josephus(int n, int k) {
	if (n == 1) {
		return 1;
	} else {
		return (josephus(n - 1, k) + k - 1) % n + 1;
	}
}

The output comes after running any of the above codes (non-recursive or recursive):

Winner is 4
Winner is 4
Winner is 3
Winner is 4

Source Code

Download

Roy Tutorials